[일반균형이론] 여러가지 효용함수의 일반균형 유도

이전 시간에는 여러가지 효용함수가 조합될 때 계약곡선의 형태에 대해 알아봤었습니다.

​

[일반균형이론] 여러가지 효용함수의 계약곡선 유도 : https://fromonetoten.tistory.com/89

[일반균형이론] 여러가지 효용함수의 계약곡선 유도

 

 

이번 시간에는 여러 효용함수가 조합될 때 일반균형이 어떻게 되는지를 상대가격의 변화를 기준으로 살펴보겠습니다.

​

​

​

1. A : 콥더글라스, B : 콥더글라스

​

일반균형을 특정하기 위해 효용함수와 부존제약이 다음과 같다고 해보겠습니다.

이제 위 제약을 바탕으로 각 개인의 효용극대화식을 세우면 다음과 같습니다.

​

이제 한계대체율을 활용하여 수요함수를 구하면 되는데, 콥-더글라스 효용함수의 수요함수를 구하는 법은 아래 글을 참고하면 됩니다.

 

[소비자이론] 보통수요함수와 보상수요함수 : https://fromonetoten.tistory.com/18

[소비자이론] 보통수요함수와 보상수요함수

 

​

그래서 계산하면 다음과 같습니다.

초과수요합이 0이 되어야 하므로, 상대가격의 크기는 다음과 같습니다.

이를 대입하면, XA=5.5 XB=4.5 YA=5.5 YB=4.5임을 알 수 있고, 이를 그래프 상으로 표현하면 다음과 같습니다.

​

​

2. A : 레온티에프, B : 레온티에프

부존제약을 바탕으로 효용극대화 식을 세우면 다음과 같습니다.

​

레온티에프의 수요함수도 위의 여러가지 수요함수를 구하는 방식을 통해서 알 수 있습니다.

​

결과적으로 수요함수는 다음과 같습니다.

​

그런데 이 수요함수인 경우 두 수요의 합이 1로 항상 일정합니다. 즉 초과수요가 없습니다.

​

이 뜻은 레온티에프의 경우, 항상 초과수요가 발생하지 않음을 의미합니다.

​

초과수요가 발생하지 않으므로 계약이 성립만한다면 일반균형이 되므로, 이 경우 일반균형은 계약곡선을 범위로 하게 됩니다.

​

3. A : 레온티에프, B : 선형

​

구체적으로 일반균형을 찾기 위해 두 경제주체 A와 B가 두 재화 V와 F에 대한 효용함수와 부존량을 다음과 같이 상정하겠습니다.

​

이제 A와 B의 수요함수를 도출하면 다음과 같습니다.

이때 각 개인에 대해서 하나의 재화수요함수만 유도하면 다른 재화는 자연스럽게 구할 수 있으므로 하나씩만 구하면 되겠습니다.

​

이제 각 재화별 가격(상대가격)에 따라 초과수요의 크기를 계산해서 초과수요가 0이 되는 가격수준이 일반균형이 됩니다. 이 예시에서는 선형효용함수의 수요함수가 상대가격의 크기에 따라 수요가 극단적으로 변하므로 선형효용함수의 수요함수를 기준으로 생각하면 다음과 같습니다.

​

​

따라서 총초과수요의 합이 0이 되게 하는 가격 수준인 PV/PF = 2일 때가 균형가격이 되고, 이때 일반균형은

VA=35, VB=65, FA=70, FB=30이 됩니다. 이를 그래프로 표현하면 다음과 같습니다.

​

​

​

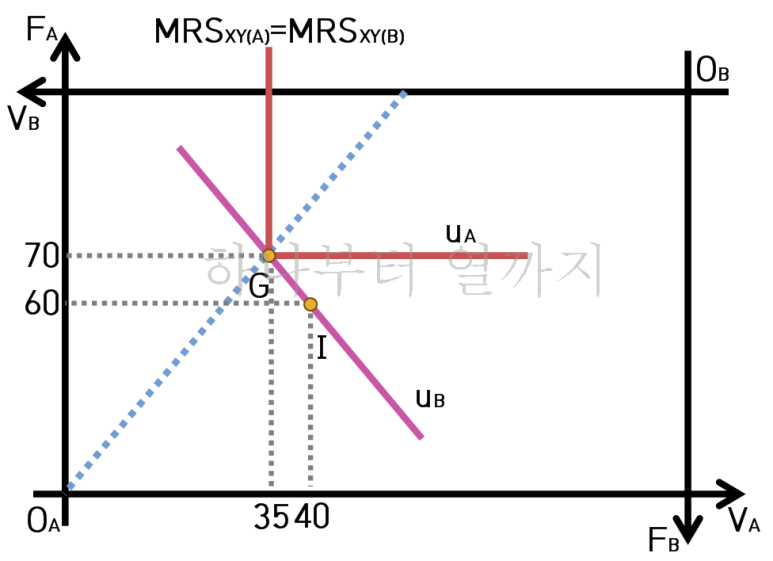
4. A : 선형, B : 선형

​

효용함수와 부존량의 배분이 다음과 같이 되어있다고 가정해 보겠습니다.

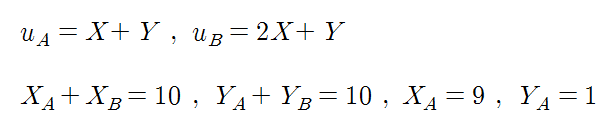
이 상태에서 경제주체 A와 B의 효용극대화 식은 다음과 같습니다.

​

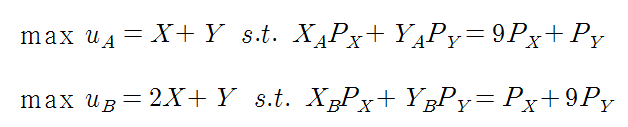
선형 효용함수이므로 상대가격의 크기에 따라서 구간별로 수요함수가 결정됩니다. 그러면 다음과 같습니다.

​

​

두 수요함수를 보았을 때, 상대가격의 크기가 1과 2를 기준으로 다음과 같이 나눌 수 있습니다.

​

위 결과를 통해서 상대가격이 1일 때, 초과수요가 0이됨을 알 수 있습니다.

​

그리고 이때, XA=0, XB=10, YA=10, YB=0이 됩니다.

여기까지 여러 가지 형태의 효용함수 상황에서 일반균형을 구해봤습니다.

​

익숙해지기만 하면 어려운 부분은 아니므로 차근차근 따라오면 이해하실 수 있을거라 생각합니다.

​

다음 시간에는 불완전 경쟁 하에서 순수교환경제 모형을 살펴보겠습니다.

​

​

궁금하거나 지적할 부분이 있으면 언제든 댓글 달아주세요~