[게임이론] 혼합전략내쉬균형

지난 시간에 우리는 순수전략균형의 일종으로서 우월전략균형과 내쉬균형을 살펴보았습니다.

​

이번 포스트에서는 참여자들이 여러 행동을 확률적으로 섞어 만든 혼합전략균형에 대해 알아보겠습니다.

​

​

​

혼합전략균형은 참여자들이 여러 전략들을 확률에 따라 선택하였을 때 그 조합된 전략묶음을 가리킵니다. 그리고 이 중 자신에게 최적의 보수를 제공하는 내쉬균형을 혼합전략내쉬균형(Mixed Strategy Nash Equilibrium; MSNE)이라고 합니다.

​

​

​

혼합전략내쉬균형은 그 취지상 순수전략내쉬균형이 없을 때 활용됩니다. 왜냐하면 순수전략으로서 내쉬균형이 존재한다면 상대방의 반응 확률을 고려할 필요 없이 자신의 최적전략을 일관되게 밀어붙이면 되기 때문입니다.

​

​

​

이제 두 가지 정규형 게임의 사례를 통해 혼합전략 내쉬균형에 대해 구체적으로 살펴보겠습니다.

​

​

​

1. 순수전략 내쉬균형이 존재하지 않는 경우

지난 시간에 살펴본 것과 같이 이 보수행렬에서 내쉬균형은 존재하지 않습니다.

​

​

​

이제 참여자 A가 S1을 택할 확률을 p라고 두면, S2를 택할 확률은 1-p가 됩니다. 또한, B가 S1을 택할 확률을 q라고 두면 S2를 택할 확률은 1-q가 됩니다. 그러면 각 참여자들의 전략 선택은 서로 독립사건이므로 각 사건별로 선택확률은 다음과 같습니다.

​

이때 경기자 A의 기대보수는 다음과 같습니다.

​

위 수식에 따라 q=1/2일 때, 자신의 이윤이 극대화됨을 알 수 있습니다.

​

​

그리고 q<1/2이면 편미분값이 반드시 0보다 작게 되는데 이는 p가 작을수록 보수가 커진다는 의미이므로 이때 최적은 p=0입니다.

​

​

반대로 q>1/2이면 편미분값이 반드시 0보다 크므로 p가 크면 클수록 보수가 높아지므로 p=1일 때 보수가 가장 높아집니다.

​

​

이제 바꿔서 경기자 B의 입장에서도 기대보수를 구하면 다음과 같습니다.

​

​

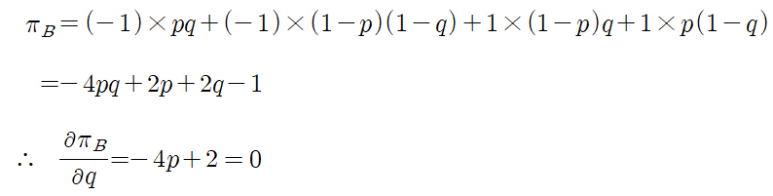
따라서 역시 B도 p=1/2일 때 이윤이 극대화됨을 알 수 있습니다.

​

​

그리고 p<1/2이면 편미분값이 반드시 0보다 크게 되는데 이는 p가 클수록 보수가 커진다는 의미이므로 이때 최적은 q=1입니다.

​

반대로 p>1/2이면 편미분값이 반드시 0보다 작으므로 p가 크면 클수록 보수가 작아지므로 q=0일 때 보수가 가장 높아집니다.

​

​

이를 p와 q를 축으로 하는 그래프로 나타내면 다음과 같습니다.

​

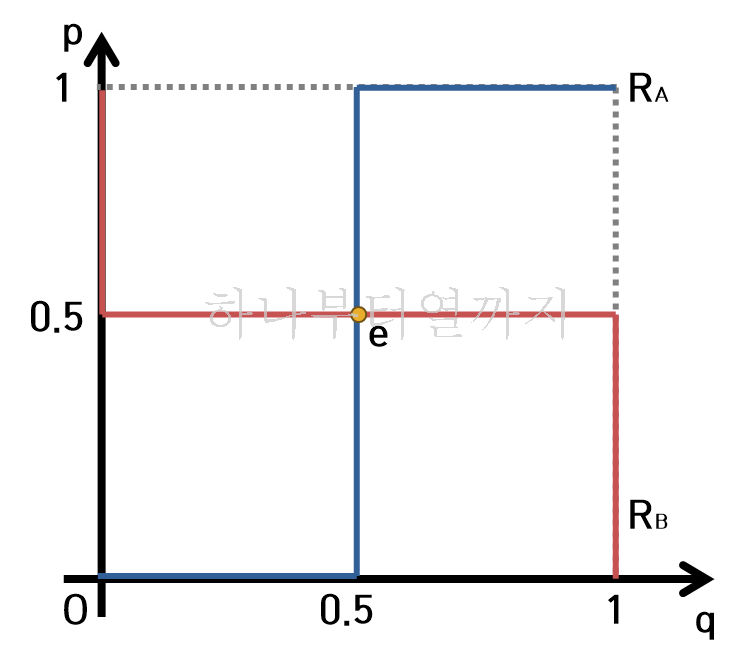
이때 나타나는 각 경기자의 최적 확률 조합을 나타낸 선을 반응곡선(Reaction curve)이라고 하며, 위 그래프에서는 각각 RA, RB로 나타나 있습니다.

​

반응곡선의 의미는 상대방의 확률에 따라 자신의 최적 전략선택확률을 그래프로 나타낸 것이라고 보면 됩니다. 따라서 반응곡선의 교점에서 자신과 상대방의 전략 선택확률이 동일해지므로 혼합전략의 균형이 된다고 할 수 있습니다.

​

위 경우에서는 e점인 p=0.5 q=0.5인 경우에 혼합전략내쉬균형을 달성함을 알 수 있습니다.

​

​

2. 순수전략 내쉬균형이 존재하는 경우

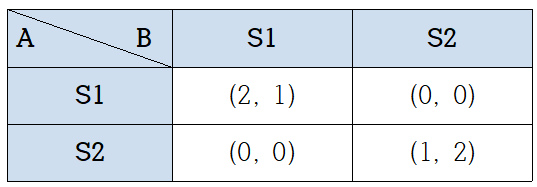
이번에는 순수전략 내쉬균형이 존재하는 경우에 대해서 반응곡선을 활용해 혼합전략 내쉬균형을 찾아보겠습니다.

​

위의 정규형 게임에서 순수전략 내쉬균형은 (S1, S1) 과 (S2, S2)입니다.

​

이와 무관히 반응곡선을 구하는 것은 각 개인이 얻을 것이라 생각하는 기대보수를 극대화하는 것입니다.

​

참여자 A가 S1을 택할 확률을 p, 참여자 B가 S1을 택할 확률을 q라고 하면 확률은 다음과 같습니다.

​

​

이제 각 확률에 따른 A의 기대보수의 크기는 다음과 같습니다.

​

따라서 q=1/3을 기준으로 보았을 때,

q>1/3이면 편미분 값이 0보다 크므로, p가 클수록 A의 보수가 커집니다. 따라서 p=1

q<1/3이면 편미분 값이 0보다 작으므로, p가 작을수록 A의 보수가 커지므로, p=0

​

마찬가지로 B의 기대보수의 크기는 다음과 같습니다.

​

​

p=2/3를 기준으로,

p>2/3이면 편미분 값이 0보다 크므로, q가 클수록 B의 보수가 커집니다. 따라서 q=1

p<2/3이면 편미분 값이 0보다 작으므로 q가 작을수록 B의 보수가 커집니다. 따라서 q=0

​

이제 위 내용을 반영하여 반응곡선을 그리면 다음과 같습니다.

​

이 반응곡선에서 알 수 있듯이 순수전략 내쉬균형도 혼합전략 내쉬균형의 하나로 포함되며, 순수전략에서는 확인할 수 없었던 균형 e를 찾아낼 수 있습니다. 그래서 혼합전략 내쉬균형에서 균형의 수는 (p, q) = (0,0), (2/3, 1/3), (1,1)로 세 개입니다.

​

​

일반적인 게임에서 반드시 혼합전략내쉬균형은 하나 이상은 존재합니다. 또한 순수균형이 아닌 혼합균형에서는 편미분값이 0이므로 상대방이 어떤 선택을 하든 자신의 보수를 무차별하게 만들 수 있습니다.

​

​

​

다음 시간에는 순차게임의 의미와 균형을 찾아내는 방법을 알아보겠습니다.

​

​

궁금하거나 지적할 사항이 있는 경우 댓글 남겨주시면 확인하도록 하겠습니다. 감사합니다.

​