[게임이론] 우월전략균형과 내쉬균형, 용의자의 딜레마

이전 시간에 게임이론의 기본적인 내용을 알아보았다면, 이번 시간에는 순수전략균형 중 우월전략균형과 내쉬균형을 살펴보고, 대표적 예시인 용의자의 딜레마에 대해서 설명하겠습니다.

​

순수전략균형에 대해서 살펴보기 전에 먼저 순수전략과 혼합전략에 대해서 설명하겠습니다. 순수전략은 선택한 전략이 확률에 관계없이 일정하게 정해져 있는 것을 말하고, 혼합전략은 여러 개의 순수전략을 확률에 따라서 선택하는 경우를 말합니다.

​

순수전략의 균형은 여러 가지가 있는데 대학에서는 보통 우월전략균형과 내쉬균형을 배웁니다.

​

​

1. 우월전략균형(dominant strategy equilibrium)

​

​

우월전략균형이란 상대방의 전략과 관계없이 자신의 보수가 극대화되는 전략의 조합을 가리킵니다.

​

​

자신의 전략을 Si, 상대방의 전략을 S-i, 그 때 자신이 얻는 보수를 ui라고 할 때, 우월전략균형에서는 다음이 성립합니다.

우월전략균형은 다음과 같은 경우입니다.

이 게임에서 알 수 있는 것처럼 상대방이 협동을 하든 경쟁을 하든 협동을 하는 것이 우월 전략입니다. 그리고 이 우월전략으로 만들어진 균형이 우월전략균형입니다.

​

따라서 우월전략균형은 각 참가자에게 우월전략은 하나이므로, 존재한다면 유일한 균형입니다. 물론 존재하지 않을 수도 있습니다.

​

또한 존재한다면 굉장히 안정적인 균형입니다. 어느 누구도 균형에서 이탈할 유인이 없습니다.

​

​

​

하지만, 우월전략균형이 사회적으로 최적의 균형은 아닙니다. 대표적인 예시가 용의자의 딜레마입니다.

​

​

​

2. 용의자의 딜레마(죄수의 딜레마, Prisoner's dilemma)

​

두 용의자(참여자) A, B가 서로 의사소통할 수 없는 상황에서 두 가지 행동 중 선택해야 하는 상황이라고 해보겠습니다.

​

자백(Confess) : 자신의 죄를 자백

​

부인(Deny) : 자신의 죄를 부인

​

둘 다 부인하면 경범죄로 낮은 형량을 받게 되어 8의 효용을 얻는다고 가정합니다. 또 둘 다 자백하면 정상적인 형량을 받게 되어 4의 효용을 얻습니다. 그리고 한 명이 자백하고 한 명이 부인하면 자백한 사람은 사법거래로 무죄가 되어 10의 효용을 얻고 부인한 사람은 징벌적 형량으로 1의 효용을 얻는다고 하겠습니다. 이를 표로 나타내면 다음과 같습니다.

​

이 때 각 개인은 상대방의 전략과 관계없이 자백(Confess)하는 것이 최선의 전략이 됩니다. 따라서 (자백, 자백)이 우월전략균형이 됩니다. 두 참여자의 효용을 모두 높일 수 있는 (부인, 부인)이라는 선택지가 있음에도 불구하고 우월전략균형이 되지 못한다는 것은 사회적으로 최적 균형과 사적인 최적 균형이 서로 일치하지 않을 수 있음을 뜻합니다. 이런 상황을 용의자의 딜레마라고 합니다.

​

이렇게 사적 균형과 사회적 균형이 일치하지 못하는 것은 크게 두 가지 이유로 정리됩니다. 한 가지는 각 경기자를 구속할 수 있는 계약이나 협약이 존재하지 않습니다. 이때문에 각 경기자들은 상대방이 자신의 이익을 극대화한다고 가정하고, 자신의 전략을 구사할 수밖에 없습니다. 따라서 구속력 있는 계약이나 법규가 있다면 이들의 후생이 개선될 수 있습니다.

​

다른 하나는 사회적으로 권장되지 않는 행동에 대해 더 높은 보수가 주어지는 보수체계 때문입니다. 사회적으로 분명히 더 이익이라면 사회적으로 최적의 결과가 사적으로도 최적이 되게끔 제공되어야 합니다.

​

​

​

​

3. 내쉬균형(Nash equilibrium)

​

내쉬균형이란 상대방의 전략이 주어진 것으로 보았을 때 자신에게 최적인 전략을 내쉬전략이라고 합니다. 그리고 이렇게 각 경기자들의 내쉬전략의 합으로 구성된 균형을 내쉬균형이라고 합니다. 내쉬균형은 각 경기자의 최적전략을 전제로 자신의 최적전략을 구성한 것이기 때문에 안정적인 균형입니다. 또한 내쉬균형은 존재하지 않을 수도 있고 한 개 또는 여러 개의 균형이 있을 수도 있습니다.

​

​

내쉬균형을 수식으로 나타내면 다음과 같습니다.

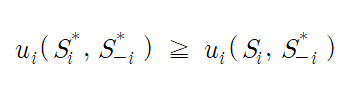
내쉬균형의 존재여부에 대해 여러 케이스들을 통해 살펴보겠습니다.

​

​

​

1) 내쉬균형이 존재하지 않는 경우

앞에서 몇 번 살펴봤었던 케이스를 다시 한 번 보겠습니다.

​

내쉬균형이 되려면 상대방의 전략이 주어졌을 때, 나의 최적 전략이 존재해야 하며 그 균형이 유지되어야 합니다.

​

예를 들어 참여자 B의 입장에서 오른쪽을 택했을 때, A는 오른쪽을 택하는 것이 최적전략입니다. 만약 (오른쪽, 오른쪽)이 내쉬균형이 되려면 이 상태가 유지되어야 하는데, B는 A가 오른쪽을 택했을 때 왼쪽으로 선택을 바꾸는 것이 유리하므로 (오른쪽, 오른쪽)은 내쉬균형이 되지 못합니다.

​

마찬가지로 B가 왼쪽을 택했을 때, A는 왼쪽을 택하는 것이 최적 전략인데 (왼쪽, 왼쪽) 상황에서 B는 자신의 전략을 바꾸는 것이 최적이므로 역시 내쉬균형이 아닙니다.

​

반대로 했을 때도 (오른쪽, 왼쪽) 또는 (왼쪽, 오른쪽) 모두 내쉬균형이 아님을 알 수 있습니다.

​

​

그래서 이 게임에서는 내쉬균형은 존재하지 않습니다.

​

​

​

2) 여러 개의 내쉬규형이 존재하는 경우

A가 전략을 S1을 택했다고 할 때, B는 S1을 택하는 것이 최선입니다. 한편 B가 S1을 택했을 때 A는 자신의 전략을 S1에서 바꿀 유인이 없습니다. 따라서 (S1, S1)은 안정적인 균형인 내쉬균형에 해당합니다.

​

그런데 A가 전략을 S2로 택했을 때, B는 S2를 택하고 이 역시 마찬가지로 A가 자신의 전략을 다시 바꿀 유인이 없으므로 (S2, S2)도 역시 균형입니다.

​

이 게임에서 내쉬균형은 (S1,S1), (S2,S2)로 두 개 존재합니다.

​

하지만 이 두 균형 중에서 (S1, S1)은 (S2, S2)보다 각 개인이 얻는 이익이 더 크므로 사적으로 바람직합니다. 또한 보수의 총합이 더 크므로 사회적으로도 바람직합니다.

​

​

​

3) 하나의 내쉬균형이 존재하는 경우

​

앞에서 봤던 용의자의 딜레마에 해당하는 게임이 대표적으로 하나의 내쉬균형이 존재하는 케이스입니다.

​

상대방이 Deny 전략을 쓰게 되면 참여자는 Confess를 쓰는 것이 합리적이고, Confess가 구사될 경우 상대방은 Confess로 대응하는 것이 최적입니다. 그리고 (Confess, Confess)에서 더 이상 전략의 변화가 없으므로 해당 전략이 균형 전략이 됩니다.

​

그래서 이 게임의 내쉬균형은 (Confess,Confess)로 한 개 존재합니다.

​

​

여기서 알 수 있는 사실이 우월전략균형이면 내쉬균형이 성립합니다. 우월전략균형은 상대의 전략과 관계없이 나의 최적전략을 찾는 것이므로 내쉬균형보다 더 강한 조건이라고 할 수 있습니다. 그래서 우월전략균형은 내쉬균형에 해당합니다.

​

그리고 내쉬균형은 여러 개가 있는데, 그 중에 일부 균형은 다른 균형보다 파레토우월한 균형이 있을 수 있습니다. 우리는 그런 균형을 초점(Focal point)이라고 합니다.

​

​

​

4. 그 외의 전략균형들

​

우월전략균형이나 내쉬전략균형이 보통 다룰 수 있는 게임의 균형입니다.

​

물론 이 외에도 참가자의 성향이나 방식에 따라 여러 가지 균형을 생각해볼 수 있습니다.

​

대표적인 것이 최소극대화전략(maximin strategy)입니다.

​

최소극대화 전략은 자기가 얻을 수 있는 보수의 최솟값을 극대화시키는 전략입니다. 이는 상대방이 어느 정도 비합리적이라고 움직일 수 있다는 점을 염두에 두고, 자신의 이익을 최대한 지키기 위한 보수적이고 위험기피적인 전략이라고 평할 수 있습니다.

​

예를 들어 다음의 정규형 게임을 생각해보겠습니다.

이 게임에서 먼저 내쉬균형을 찾아보겠습니다.

​

1) 내쉬균형 : A가 S1을 택할 때, B의 최적전략은 S2입니다. 그리고 이때 A의 최적전략은 S2가 됩니다. 이후 B는 자신의 전략을 바꿀 유인이 없으므로 (S2, S2)가 유일한 내쉬균형이 됩니다.

​

2) 최소극대화 전략

A가 B의 합리성에 대해서 의심하여 최소극대화전략을 취할 경우 S1의 최솟값은 1이고, S2의 최솟값은 -10이므로 A는 S1을 택하게 됩니다.

​

B도 최소극대화전략을 취할 경우 S1의 최솟값은 2이고, S2의 최솟값은 4이므로 S2를 택합니다.

​

따라서 최소극대화전략에 따른 균형은 (S1, S2)가 됩니다.

​

이렇게 최소극대화전략을 택하는 경우는 대개 상호생존의 위협이 있을 경우, 자신이 입을 회복불가능한 피해를 막기 위한 때에 활용가능합니다.

​

​

여기까지 순수전략균형과 용의자의 딜레마 개념에 대해서 살펴보았고, 다음 포스트에서는 혼합전략균형에 대해서 알아보겠습니다.

​

궁금하거나 지적할 사항은 댓글로 알려주세요