[소비자이론] 간접효용함수와 지출함수

이번 글에서는 간접효용함수와 지출함수에 대해서 살펴보고 지난시간에 알아본 보통수요함수 및 보상수요함수와 쌍대성 측면에서 그 관계를 살펴보겠습니다.

​

간접효용함수(indirect utility function;V)란 주어진 가격과 예산제약 하에서 실현가능한 최대효용을 나타내는 함수입니다. 그래서 이 함수는 효용을 가격과 소득으로 나타냅니다.

​

반면 지출함수(expenditure function;E)는 일정한 효용하에서 지출을 극소화시키는 함수를 말합니다. 그래서 이 함수는 지출을 가격과 효용으로 나타냅니다.

​

계산은 간단합니다.

​

간접효용함수는 효용극대화를 통해 구한 x, y의 최적값을 효용함수에 대입하며, 지출함수는 지출극소화를 통해 구한 x, y의 최적값을 지출식에 대입합니다.

​

그런데 수요함수와 보상수요함수가 각각 효용극대화와 비용극소화를 통해 유도되므로,

​

효용함수 식에 수요함수 식을 대입하면 간접효용함수가 나오고, 예산제약식에 보상수요함수를 넣으면 지출함수가 도출된다고 이해하셔도 됩니다.

​

​

​이하에서는 기본적인 형태의 효용함수의 간접효용함수와 지출함수를 구해보겠습니다.

​

1. 콥더글라스 효용함수의 간접효용함수, 지출함수

위 식에서 보는 바와 같이 효용극대화 조건에서 보통수요함수를 유도한 뒤에 이를 목적식인 효용함수에 대입하면, 간접효용함수가 도출됩니다.

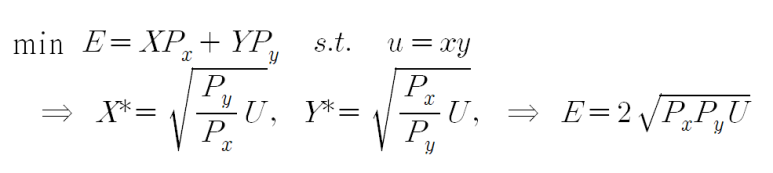
반대로 지출극소화 조건에서 보상수요함수를 유도한 뒤 이를 목적식인 예산제약식에 대입하면 지출함수가 됩니다.

​

2. 레온티에프 효용함수의 간접효용함수, 지출함수

3. 선형 효용함수의 간접효용함수, 지출함수

선형 효용함수는 그 수요함수와 보상수요함수가 구간별로 다르게 나타나므로, 간접효용함수와 지출함수도 구간에 따라 나뉩니다만, 별도로 유도하지는 않겠습니다.

​

4. 준선형 효용함수의 간접효용함수, 지출함수

​

다음 결과를 정리하면 아래와 같습니다.

여기서 주목할 사실은 간접효용함수를 소득에 대한 함수로 정리하면 지출함수가 된다는 것입니다!

​

예를 들어 콥더글라스 간접효용함수를 소득을 기준으로 다시 정리하면,

​

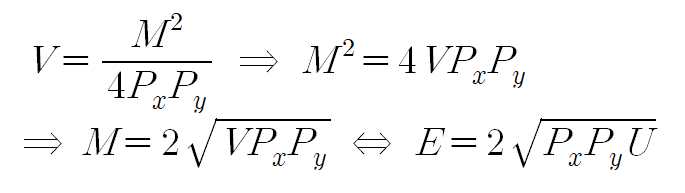
이는 지출함수와 간접효용함수는 동전의 양면과 같아서 하나가 유도되면, 나머지 하나가 자동으로 유도되는 쌍대성 관계가 성립한다고 볼 수 있습니다.

​

쌍대성에 대한 논의는 이전 글을 참고하시면 되겠습니다.

​

 

[소비자이론] 효용극대화와 비용극소화, 그리고 쌍대성 : fromonetoten.tistory.com/11

 

 

그리고 여기에서 나오는 로이의 항등식과 셰퍼드 정리는 수요함수 및 보상수요함수에서 간접효용함수나 지출함수를 유도할 수 있습니다.

이는 보통수요함수나 보상수요함수에서 간접효용함수와 지출함수를 유도하는데, 그 역과정으로서 의미를 갖습니다.

​

1) 로이의 항등식(Roy's identity) : 간접효용함수 → 수요함수 도출

​

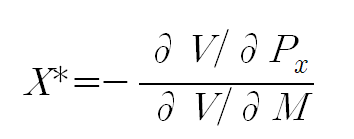
2) 셰퍼드의 정리(Shephard's lemma) : 지출함수 → 보상수요함수 도출

​

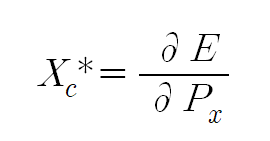
다음 포스트에서는 보상변화와 대등변화에 대해서 알아보겠습니다.

​

​

​

궁금한 사항이나 수정이 필요한 부분이 있을 경우 댓글로 알려주시면 반영할 수 있도록 하겠습니다.