[소비자이론] 보상변화와 대등변화

이번 글에서는 보상변화와 대등변화에 대해 알아보겠습니다.

​

보상변화(Compensating Variation;CV)란 가격변화에도 불구하고 원래 효용을 일정하게 유지하기 위해서 필요한 소득의 변화량을 가리킵니다. 즉 최초 수준으로 유지하는데 드는 소득의 크기입니다.

​

대등변화(Equivalent Variation;EV)는 가격변화가 없으나, 가격이 변화했을 때 나타나는 효용을 달성하기 위해서 필요한 소득의 크기입니다. 즉 목표 효용을 달성하기 위해 현 가격체계에서 요구되는 소득을 말합니다.

​

이 개념을 그래프를 보면서 구체적으로 이해해보도록 하겠습니다.

​

최초 가격체계 P0에서 효용 U0에 대해서 선택점 E0이고, 변화된 가격체계 P1에서 효용U1에서 선택점이 E1입니다.

​

이때 E'0는 E0에서 대체효과에 따른 이동점이고, E'1은 E1에서 대체효과에 따른 이동점입니다.

​

​

보상변화는 변화된 가격체계 P1에서 최초효용 U0를 유지하기 위해서 보조하는 소득의 크기입니다.

​

즉 위 그래프에서 CV만큼 소득이 줄어든다면 변화된 가격체계에서도 U0가 최적이 될 것입니다.

​

그리고 이때 최적점의 위치는 E'0입니다.

​

​

반면 대등변화는 최초 가격체계 P0에서 변화된 효용 U1을 달성하기 위해 보조하는 소득의 크기입니다.

​

이 경우 위 그래프에서 EV만큼 소득이 늘어난다면 최초 가격체계에서도 U1이 최적이 될 것입니다.

​

그리고 이때 최적점의 위치는 P'1입니다.

​

​

여기에서 우리는 몇 가지 사실을 알 수 있습니다.

​

a. E0, E1간에 보상변화와 대등변화를 구할 경우 두 값의 부호는 반대입니다.

​

b. 보상변화와 대등변화는 그 정의상 지출함수 E를 활용하여 다음과 같이 구할 수 있습니다.

​

예컨대 보상변화는 가격이 바뀌었음에도 불구하고 최초 효용을 유지하는 데 드는 소득이므로 정의상 E(P0,U0)-E(P1,U0)가 성립합니다. 그런데 상대가격의 변화만 있을 뿐 명목소득의 변화는 없으므로 E(P0,U0)=E(P1,U1)가 성립하므로 이를 대입하면 E(P1,U0)-E(P0,U0)가 성립합니다.

​

대등변화에 대해서도 마찬가지로 변화된 효용을 달성하기 위해 최초 가격수준에서 드는 소득이므로 E(P0,U1)-E(P1,U1)인데 E(P1,U1)=E(P0,U0)이므로 위 식이 성립합니다.

​

그래서 보상변화와 대등변화의 개념을 두 번째 등식을 중심으로 생각해보면

​

보상변화는 가격변화로 인한 효용 변화를 변한 가격을 기준으로 측정한 것과 같으며,

대등변화는 가격변화로 인한 효용 변화를 원래 가격을 기준으로 측정한 것과 같습니다.

​

c. 보상변화와 대등변화의 값 크기가 일반적으로 같지 않습니다.

​

그 이유를 좀 더 자세하게 살펴보겠습니다.

위 그래프에서 보면 보상변화는 가격이 바뀜에도 불구하고 초기효용을 유지하는 것이므로 보상수요곡선 Dc0상에서의 면적이 보상변화의 크기가 됩니다.(CV=α)

​

반면 대등변화에서는 변화된 효용을 기준으로 하므로 보상수요곡선 Dc1상에서의 면적이 대등변화값입니다.

(EV=α+β+γ)

​

이를 수식으로 나타내면 아래와 같습니다.

​

그러면 이제 궁금한 점은 왜 두 값이 달라지는가가 될 것입니다. 이 내용은 레온티에프 효용함수와 준선형 효용함수를 이용해 알아봅시다.

​

1. 레온티에프 효용함수의 보상변화, 대등변화(대체효과 제거)

우리가 앞서 가격효과에서 살펴본 것처럼 레온티에프 효용함수에는 대체효과가 존재하지 않습니다.

​

그래서 소득효과만의 영향을 분석하는 데 레온티에프 효용함수는 유용하게 쓰일 수 있습니다.

​

위 그래프에서처럼 U0를 유지하기 위한 소득의 크기가 CV이고, 이는 보상수요곡선의 α에 해당합니다.

​

반면 대등변화는 U1를 달성하기 위한 소득의 크기로 보상수요곡선의 α+β+γ에 해당합니다.

​

따라서 대체효과가 없더라도 보상변화와 대등변화의 크기는 달라집니다.

​

2. 준선형 효용함수의 보상변화, 대등변화(소득효과 제거)

​

​

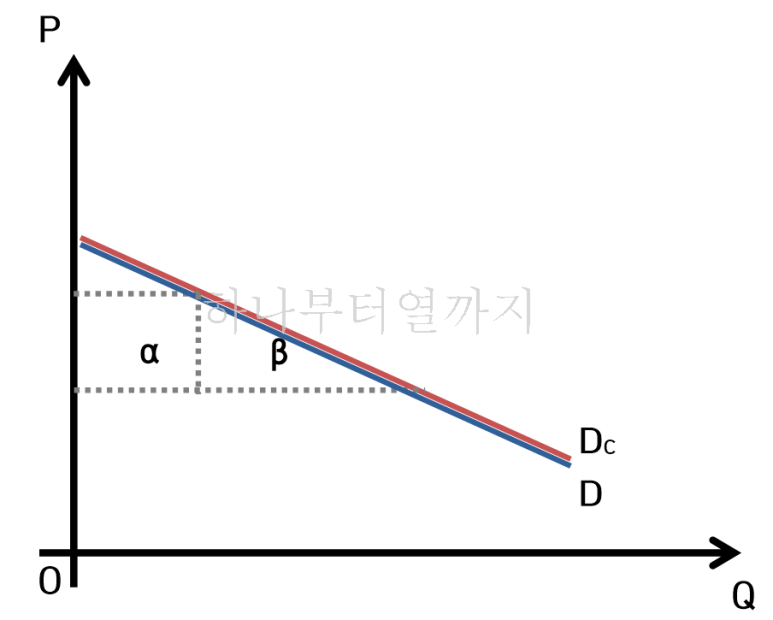
반면 준선형 효용함수는 소득효과는 없이 오로지 대체효과만 존재합니다.

​

이 경우에 보상변화와 대등변화의 크기는 동일합니다. 왜냐하면 소득효과가 없을 경우 통상수요함수와 보상수요함수는 동일하게 되며 이렇게 되면 보상변화이든 대등변화이든 그 크기는 α+β가 됩니다.

​

위 두 사례를 통해 보상변화와 대등변화의 크기 차이는 소득효과로 인해 발생한다는 사실을 알 수 있습니다.

​

특히 가격하락으로 효용이 증가할 경우 대등변화가 보상변화보다 무조건 크다는 것을 알 수 있는데 이를 재화별 특성과 가격요인을 고려하여 정리하면 아래 표와 같습니다.

​

아래 표의 크기 비교는 절댓값을 기준으로 합니다.

여기서 CV는 보상변화, EV는 대등변화이고, CS는 소비자잉여를 말합니다.

​

소비자잉여(Consumer Surplus;CS)란 구입자의 지불용의 금액에서 실제 지불금액을 제외한 것으로 소비자 잉여는 보상수요곡선과 가격 사이의 면적으로 구해집니다. 소비자 잉여에 대한 자세한 내용은 시장균형이론에서 다루도록 하고 여기서는 결론만 알고 넘어가도록 합시다.

​

​

​

다음 시간에는 현금보조, 현물보조, 가격보조를 서로 비교해보고 리베이트와 이부가격제 등 다양한 사회복지제도를 알아보겠습니다.

​

​

궁금한 점이나 수정이 필요한 부분은 언제든 댓글로 알려주시면 반영토록 하겠습니다.

​

​