[요소시장이론] 요소대체탄력성과 한계생산력이론

이번 글에서는 생산요소의 대체탄력성과 요소소득분배율,

​

그리고 요소소득의 분배와 관련된 이론인 한계생산력이론에 대해 알아보겠습니다.

​

1. 생산요소의 대체탄력성

​

생산요소의 대체탄력성(Elasticity of substitution)이란 생산자가 동일한 생산량을 유지하고 있을 때 생산요소 간에 얼마나 쉽게 대체할 수 있는지를 숫자로 나타낸 것을 말합니다.

​

이렇게 두 점 사이의 대체탄력성을 구할 수도 있으며, 한 점에서 대체탄력성은 미분을 활용하여 다음과 같이 구할 수 있습니다.

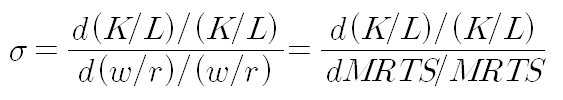
특히 한계기술대체율을 활용한 대체탄력성 공식은 균형점에서 MRTS=w/r임을 이용한 것입니다.

​

등량곡선이 많이 구부러져 있을수록(대체가 어려울수록) 대체탄력성의 크기는 감소합니다. 대표적으로 다음과 같은 생산함수는 대체탄력성이 특정값으로 일정하므로 알아두면 좋습니다.

​

또하나 알아두면 좋은 생산함수가 있는데 바로 CES 생산함수(Constant Elasticity of Substitution)입니다.

여기서 A는 임의의 상수이고, α와 ρ값도 일정 범위 내의 상수입니다.

​

이 생산함수를 알아둬야 하는 이유는 이 생산함수의 경우에도 대체탄력성이 일정하기 때문입니다.

​

2. 요소소득분배율

​

요소소득분배율은 보통 다음과 같이 정의할 수 있습니다.

노동소득과 자본소득의 비율이라고 할 수 있겠습니다. 이 요소소득분배율의 변화율과 대체탄력성과의 관계는 다음과 같습니다.

​

여기서 알 수 있는 점은 대체탄력성의 크기가 1보다 크다면, 요소소득분배율 변화율 값이 음수가 됨을 알 수 있습니다. 즉 대체탄력성이 크면 특정요소 가격의 상승이 다른 요소의 상대적인 분배몫을 줄여버릴 수 있음을 뜻합니다.

​

​

3. 소득분배의 한계생산력설(한계생산성이론, Marginal productivity theory)

​

한계생산력설이란 요소의 균형가격이 그 요소의 한계생산물가치에 의해 정해진다는 이론입니다.

​

그리고 수요 공급이 일치하는 수준에서 생산성이 정해집니다.

​

생산량과 분배량이 항상 일치해야하므로,

이므로, w=MPL, r=MPK가 성립합니다.

​

이 법칙은 각 생산요소의 분배몫은 각 요소의 한계생산성에 비례한다는 측면에서 의의가 있습니다.

​

예컨대 생산함수가 다음과 같은 콥-더글라스형태의 함수라고 해봅시다.

그러면 한계생산력설에 따르면 각 생산요소의 자원배분은 각 요소의 한계생산성에 좌우되므로 각자의 몫을 구해보면,

그래서, 노동과 자본의 배분 몫은 α:1-α 임을 알 수 있습니다.

​

그러나 이 법칙은 설명에 있어 몇 가지 한계점을 가지고 있습니다.

​

먼저 고정요소에 대한 요소가격은 설명할 수 없습니다. 그래서 고정투입요소를 설명하기 위해 지대론 등의 다른 요소이론을 도입해야 합니다.

​

다음으로 한계생산력이라는 개념을 측정하기가 어렵습니다. 한계생산성이론을 가정하고, 임금 등을 토대로 한계생산성을 추정할 수는 있지만, 그것이 임금과 일치하는지는 확인하기 어렵습니다.

​

마지막으로 산출량과 분배량이 반드시 일치하지 않는 내적정합성의 문제가 생길 수 있습니다.

​

생산함수가 만약 k차 동차함수라면, k값에 따라서 분배량과 산출량에서 차이가 나게 됩니다.

이런 문제점들이 있지만, 강력한 설명력과 기존 미시체계와의 정합성이 높기 때문에 이하의 논의에서는 특별한 경우가 아니라면 다음의 이론이 성립한다고 전제하고 이야기를 이어가도록 하겠습니다.

​

​

​

다음 시간에는 수요독점시장에 대해서 알아보겠습니다.

​

​

​

궁금하거나 지적할 사항이 있는 경우 댓글 달아주시면 반영하겠습니다.