[요소시장이론] 외생변수에 따른 요소시장 변화

이제까지 요소시장에 대해서 전반적인 내용들을 살펴보았습니다.

​

​

이번 글에서는 요소시장분석의 응용으로서, 보통 거시경제학에서 다루는 외생변수에 따른 요소시장에 어떤 충격을 주는지를 살펴보겠습니다.

​

​

여기서 우선 전제할 것은 소득분배의 한계생산력설에 따라 완전분배정리가 성립한다고 가정합니다.

​

​

따라서 다음 식을 전제로 합니다.

그리고 분석의 편의를 위해 콥-더글라스 생산함수를 가정합니다. (Q=ALαK1-α)

​

​

콥-더글라스 생산함수에서 노동과 자본의 한계생산성은 다음과 같습니다.

​

​

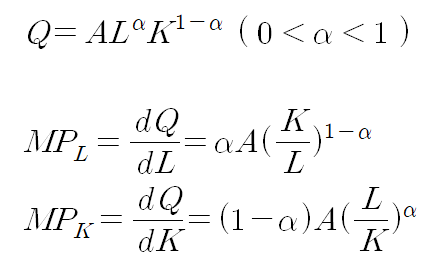
이제 변수변화에 따른 효과를 살펴보겠습니다.

​

 

 

 

​

1. 일시적 자본감소(K↓)

예컨대 자연재해로 인해 공장 시설이 파괴되는 등 외생적인 이유로 인해 자본이 일시적으로 감소하는 경우를 상정해봅시다.

​

​

자본의 크기가 다른 변수와 무관히 감소해야 하므로 여기서 자본의 공급곡선은 수직선으로 표현될 것입니다. 그 상황에서 자본의 외생적 감소는 자본수요곡선 상의 이동으로 이자율을 상승시키는 원인이 됩니다.

​

​

그리고 자본규모가 줄어들었으므로, 처음에 유도했던 MPL식을 참고하면, 노동의 한계생산성이 감소해 노동수요가 감소합니다. 따라서 임금의 크기가 줄어들게 됩니다.

​

​

​

 

 

​

2. 노동의 일시적 증가(L↑)

정부의 정책이나 기업인의 결단 등에 의해 노동공급량이 일시적으로 증가한다고 가정해보겠습니다. 노동이 일시적으로 늘어나는 경우 노동의 공급곡선상 이동에 해당하며, 임금이 하락하는 요인이 됩니다.

​

아울러 자본의 한계생산성이 늘어나게 되므로 자본에 대한 수요가 늘어나게 되고, 자본의 공급량이 정해져있다면, 이자율을 크게 상승시킬 수 있습니다.

​

​

​

 

 

​

3. 실질이자율 상승(r↑)

이자율은 자본의 요소비용입니다. 따라서 이자율의 상승은 자본의 요소비용이 상승하는 것이므로 자본시장(K-r평면)에서 MC가 상승해서 위로 상승하게 됩니다. 이에 따라 최적자본량의 크기가 줄어들게 됩니다.

최적 자본량의 크기가 하락하게 되면, 임금의 한계생산성도 같이 하락하게 되므로 노동수요가 줄어들게 되고 이는 임금 하락으로 이어집니다.

​

​

​

이번 시간까지 요소시장에 대해서 살펴보았습니다.

​

다음 시간부터는 일반균형이론에 대해서 살펴볼텐데, 먼저 일반균형의 개념적 기초를 다지는 과정을 거치도록 하겠습니다.

​

​

궁금하거나 지적할 사항이 있으신 경우, 댓글 달아주시면 답변드리겠습니다.

​